Balloon actuators

The previous two examples already showed how to use several main features of FONSim, however, the observed behaviour of the container components was rather simple. Balloon actuators provide a more interesting component and are studied extensively in the field of soft robotics (SoRo). One of their special properties is their nonlinear behaviour. On one hand this makes them somewhat difficult to use for existing applications, but it also opens a wide array of possibilities for new applications such as hardware-encoded sequencing.

PV curves

The behaviour of these balloon actuators is specified as a pressure-volume curve or pv-curve. This curve is usually derived from measurements. FONSim contains an example measurements file of a balloon actuator: Measurement_60mm_balloon_actuator_01.csv. TODO add reference to paper.

Let’s have a look at the first five lines of this CSV file:

Latex balloon actuator 60 mm,2017-11-16,MECH1A1
Time,Volume,Pressure
s,ml,mbar
14.31,1,22
17.01,2.01,280

The file is split in four parts (explained more in depth in PVCurve):

• First line: information about the file. For example, the measurement occurred in 2017, November 16.

• Second line: keys of data columns. Here we’re only interested in volume and pressure, though time is listed as well.

• Third line: units of data columns.

• Fourth line and further: the actual numerical data.

Lets read this file using FONSim and plot the curve. First, the CSV file is loaded into a PVCurve object. The resulting object has two attributes, v and p, which respectively are 1D Numpy arrays of volume and pressures. Their units have been automatically adjusted such they conform to SI base units. The pressure has also been adjusted to absolute because the measured pressure in the CSV file was relative to atmospheric pressure.

# Load pvcurve in PVCurve object
pvcurve = fons.data.PVCurve(data=ppath, pressure_reference='relative')

# Plot the curve
fig, ax = plt.subplots(1)
ax.plot(pvcurve.v * 1e6, pvcurve.p * 1e-5)
ax.set_ylabel('absolute pressure [bar]')
ax.set_xlabel('volume [ml]')
plt.show()

Full file: 06.py. The plotting result:

Figure 1: PV curve of a balloon actuator

Figure 1 shows what makes these balloon actuators so interesting: the non-monotonically increasing pressure. As a result, for some pressures there are multiple solutions for the volume of the actuator, three in this case. Note the local pressure maximum of 1.87 bar around a volume of 6 ml (the ‘hill’) and a local pressure minimum of 1.58 bar around a volume of 21 ml (the ‘dip’).

Single balloon actuator

Let’s do a simulation with this balloon actuator! Full file: 04.py.

After the usual preamble, the pressure reference and the fluid are selected:

# Pressure reference
waves = [(0, 0.890), (1, 0.650), (2, 0.550), (3, 0.650)]
wave_function = fons.wave.Custom(waves)*1e5 + fons.pressure_atmospheric

# Select a fluid
# Previous examples required a compressible fluid.
# This one doesn't, feel free to try with an incompressible fluid (e.g. water)!
fluid = fons.air

The previous required a compressible fluid as all components were constant-volume. In this example, the balloon actuators can vary their volume, so feel free to try with an incompressible fluid (for example, water)!

---

Next, the system is built and the simulation is run. The system consists of one pressure source, one balloon actuator (FreeActuator) and a tube connecting the former two.

The FreeActuator component allows to simulate components characterized by a pv-curve and therefore provides an excellent fit for simulating balloon actuators. If the pvcurve is available as a CSV file, the first two emphasized lines can be omitted and the curve filepath can be passed directly to the parameter curve of FreeActuator.

# Create system
# The FreeActuator allows to simulate components characterized by a pvcurve.
# The curve argument can take a pvcurve specified as a CSV file.
system = fons.System()
system.add(fons.PressureSource('source', pressure=wave_function))
filepath = 'resources/Measurement_60mm_balloon_actuator_01.csv'
ppath = str(ir.files('fonsim').joinpath(filepath))
system.add(fons.FreeActuator('actu', fluid=fluid, curve=ppath))
system.add(fons.CircularTube('tube', fluid=fluid, diameter=2e-3, length=0.60))
system.connect('tube', 'source')
system.connect('tube', 'actu')

# Create and run simulation
sim = fons.Simulation(system, duration=4)
sim.run()

---

Let’s plot the simulation results! Like in the previous example, we’ll use the FONSim built-in plotting functionality:

# Plot simulation results
fig, axs = plt.subplots(3, sharex=True)
fons.plot(axs[0], sim, 'pressure', 'bar', ('source', 'actu'))
axs[0].set_ylim(1.4, 2.0)
fons.plot_state(axs[1], sim, 'mass', 'g', ['actu'])
fons.plot(axs[2], sim, 'massflow', 'g/s', ['tube'])
for a in axs: a.legend()
plt.show()

This outputs the following plot figure:

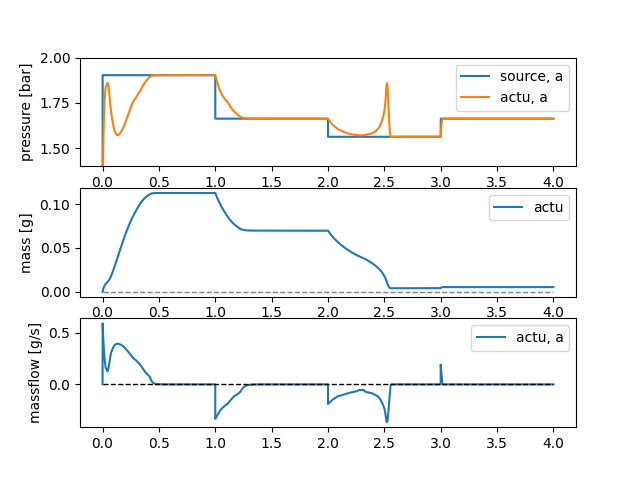
Figure 2: Simulation output

---

To finish, a brief discussion of the simulation results shown in Figure 2. The simulation starts with an increase of absolute pressure to 1.89 bar, the actuator fully inflates as this pressure is larger than the pvcurve hill. Shortly after the pvcurve has been fully inflated, the pressure decreases back to 1.65 bar, just above the pvcurve dip. The actuator therefore stays mostly inflated, as is evidenced by more than half of the mass remaining, shown in the middle graph of Figure 2.

At time = 2.0 s the pressure drops just 0.1 bar, to 1.55 bar. Nevertheless, the actuator now deflates almost fully. Increasing the pressure again at time = 3.0 s has little effect on the actuator volume (middle graph of Figure 2).

Two balloon actuators

In this second simulation, we’ll look at two balloon actuators in series and show a basic example of hardware sequencing achieved by exploiting a combination of actuator nonlinearity and flow restriction. It is based on TODO paper reference. The code is very similar to the previous simulation, so only the relevant differences are discussed here. Full file: 07.py.

Pressure reference:

# Pressure reference
p1 = 0.890
p2 = 0.650
p3 = 0.200
waves = [(0.0, p2),
         (1.0, p1), (1.3, p2),
         (3.0, p1), (3.5, p2),
         (5.0, p3), (5.3, p2),
         (7.0, p3), (7.4, p2)]
wave_function = fons.wave.Custom(waves, time_notation='absolute')*1e5\
                + fons.pressure_atmospheric

tubes:

system.add(fons.CircularTube('tube_0', fluid=fluid, diameter=2e-3, length=1.20))
system.add(fons.CircularTube('tube_1', fluid=fluid, diameter=2e-3, length=0.60))

and the plotting:

# Plot simulation results
fig, axs = plt.subplots(3, sharex=True)
fons.plot(axs[0], sim, 'pressure', 'bar', ('source', 'actu_0', 'actu_1'))
axs[0].set_ylim(1.1, 2.0)
fons.plot_state(axs[1], sim, 'mass', 'g', ['actu_0', 'actu_1'])
fons.plot(axs[2], sim, 'massflow', 'g/s', ['tube_0', 'tube_1'])
for a in axs: a.legend()
plt.show(block=False)

# Also do a parametric plot
rho = fluid.rho if hasattr(fluid, 'rho') else fluid.rho_stp
p_atm = fons.pressure_atmospheric
m_a0 = system.get('actu_0').get_state('mass')
p_a0 = system.get('actu_0').get('pressure')
v_a0 = m_a0 / rho * p_atm / p_a0
m_a1 = system.get('actu_1').get_state('mass')
p_a1 = system.get('actu_1').get('pressure')
v_a1 = m_a1 / rho * p_atm / p_a1

fig, ax = plt.subplots(1)
ax.plot(v_a0 * 1e6, v_a1 * 1e6)
ax.set_aspect('equal')
ax.set_xlabel('volume actuator 0 [ml]')
ax.set_ylabel('volume actuator 1 [ml]')
plt.show()

This gives the following two figures:

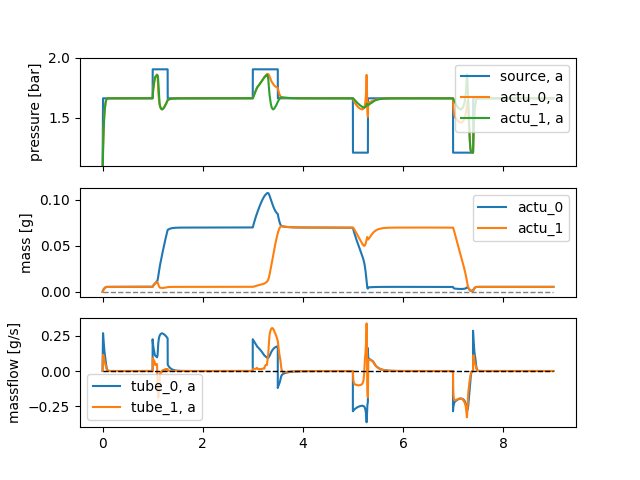
Figure 3: Simulation output

Figure 4: Simulation output, actuator volumes

---

Figures 3 and 4 show the simulation results. The middle graph of Figure 3 shows the achieved phase lag. Even while actuator 0 is inflated first, it is actuator 1 that is deflated last. Also note that the system state between the transitions is stable, as is shown by the constant pressure and mass in these region. These regions can thus be elongated or shortened by changing the pressure reference timings.

This phase lag is also well visible in Figure 4, which plots a virtual path traversed by the actuator volumes. In research work TODO, this phase lag was used to produce a stepping motion for a legged robot, where one actuator moved the feet horizontally and another one moved the feet vertically.